SHELLSPEC

Program SHELLSPEC is designed to calculate lightcurves, spectra and images of interacting binaries and extrasolar planets immersed in a moving circumstellar matter (CM). It solves a simple radiative transfer along the line of sight in 3D moving media. Roche model and synthetic spectra from the stellar atmosphere models can be used as a boundary condition for the radiative transfer. The scattered light from the two stars can be taken into account assuming that CM is optically thin. Dust, including non-isotropic Mie scattering, can also be taken into account. The assumptions include LTE and optional known state quantities and velocity fields in 3D. These can be taken from the 3D hydrodynamical simulations. Alternatively, optional (non)transparent objects such as: a central star, companion star, envelope, spot, stream, ring, disc, nebula, flow, jet, ufo, or a shell may be defined in 3D and their composite synthetic spectrum calculated. Stars may have either the Roche or spherical geometry, optional velocity or rotation, and may have spots. They are subject to the gravity darkening, limb darkening, and an irradiation effect including the heating, reflection and day-night heat redistribution. Synthetic light curves or trailing spectrograms can be produced by changing your view points on the 3D object.

The program is written in Fortran90. It does not solve the inverse problem of finding the stellar and orbital parameters of the stars and circumstellar medium. For this purpose, Mirek Broz and Janka Nemravova developed another Python tool called PyShellspec . It can calculate also synthetic interferometric observables, fit real interferometric observations, light curves and/or spectra and obtain optimal properties of the stars and circumstellar medium. There is also a GUI for ver.39 written by Marco Gomez-Munoz. Thanks once more Mirek, Janka, and Marco.

The main applications are probably in the field of interacting binaries, cataclysmic variable stars, Algol-type eclipsing binaries, and extrasolar planets but the code is a flexible tool which can be used to study a large variety of objects and effects. A more detailed description of the code is in Budaj and Richards (2004) and, more imortantly, in the updated user manuals. Output of widely used programs for stellar atmosphere synthetic spectra, SYNSPEC (Hubeny, Lanz and Jeffery, 1994), can be used as an input boundary condition. The latest version of the code which has a new model of the reflection effect is available with complete documentation and example runs here:

DOWNLOAD SHELLSPEC49.

A separate code which calculates the Roche surface and surface temperature distribution according to the new reflection effect can be found with the complete documentation and examples here: DOWNLOAD ROCHE.

Below is the schematic illustration of the new model of the reflection effect (Budaj 2011) which consist of reflection, heating and heat redistribution. It is a pole-on view of the planet irradiated by the star. Red regions on the day side are hot while yellow regions on the night side and around poles are cool due to the irradiation and zonal heat transfer. $\delta$ is irradiating angle, $A_{B}$ is Bond albedo, $P_{r}$ is heat redistribution parameter, $T_{ir}$ is temperature associated with local heating, $T_{dn}$ is associated with heat redistribution and depends on the latitude, and $T_{old}$ is associated with interior cooling and with surface temperatures in the absence of the irradiation. Roche shape of the planet corresponds to the filling factor equal to 1. Position and size of the star are not to scale.

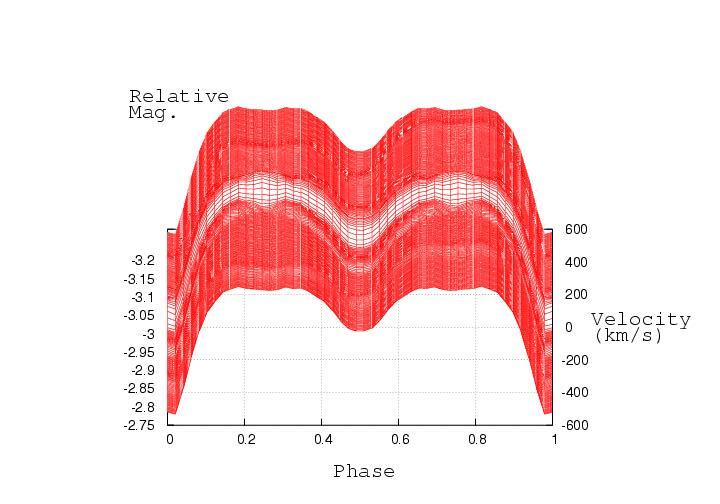
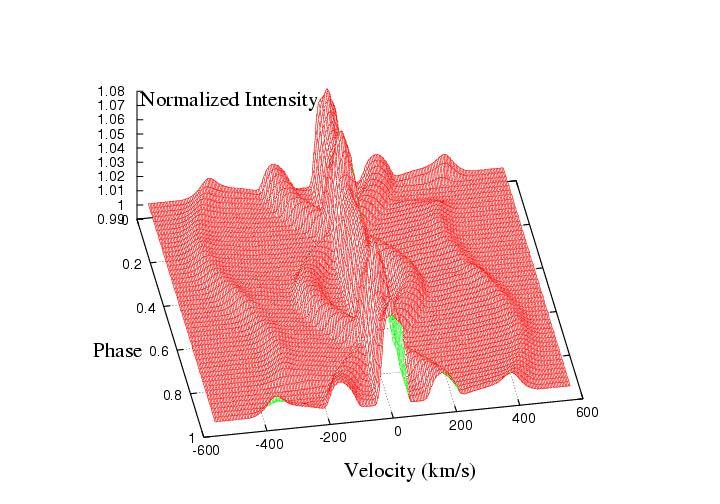
Below is the demonstration of an artificial test model and an artificial spectral line. The model includes two stars, a Keplerian equatorial disc around a bigger primary, a slightly inclined jet and a slowly expanding shell surrounding the system. Stars are treated as blackbodies, the primary is a sphere with limb darkening imposed on while the secondary fills its Roche lobe and is subject to gravity darkening only. The centers of the jets and shell have no net space velocity while the net velocity of the center of the disc corresponds to that of the primary. Jets precess with the orbital period. For the sole purpose of this illustration, the input values were manipulated so that a contribution from each object could be seen.

• Below is a 2D projection image ($I_{\nu}^{out}(x,y)$) of a test model in the continuum (at a frequency in the far wing of the spectral line). Different shapes of the primary and secondary illustrate the effects of limb darkening and gravity darkening.
• The figure below displays the spectrum of the model. The central emission comes from the slowly expanding shell. The two symmetric bumps are caused by the two jet cones. The two high velocity peaks (blue and red) originate in the disc and reflect its orbital motion tracing that of the primary. Observe how they disappear near primary minimum due to the eclipse of the approaching and receding part of the disc by the secondary star.
• The figure below shows the overall light curve of the model as it revolves with the apparent primary and secondary minima at each frequency.
• The figure below shows the trailed spectrogram of the model. Observe the same features as in the movie of the spectra above.
• Contact: budaj@ta3.sk

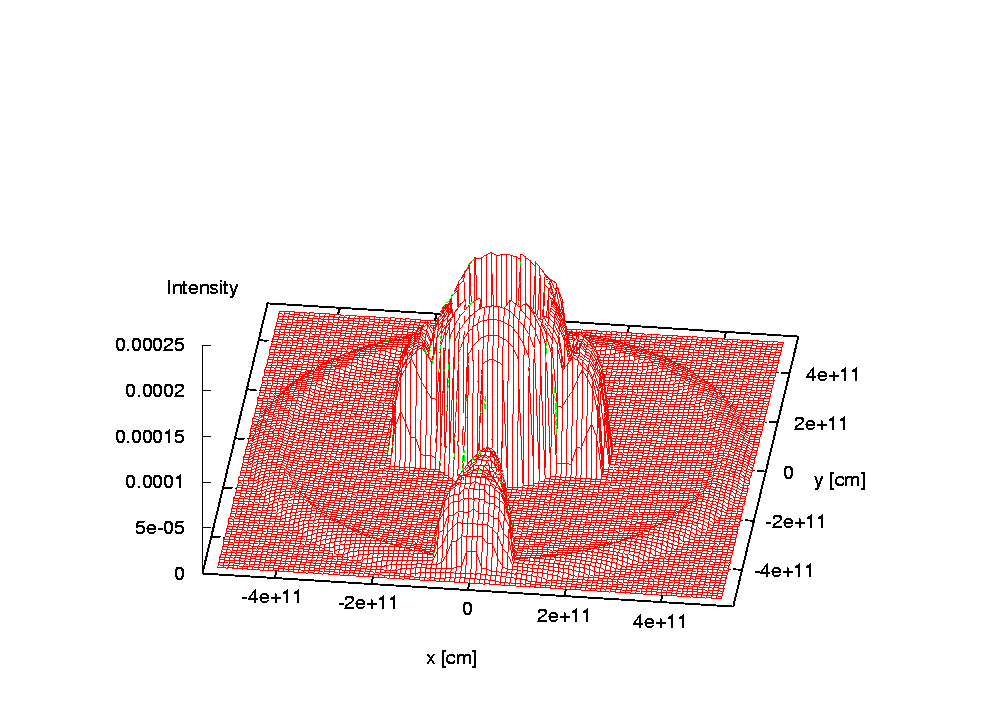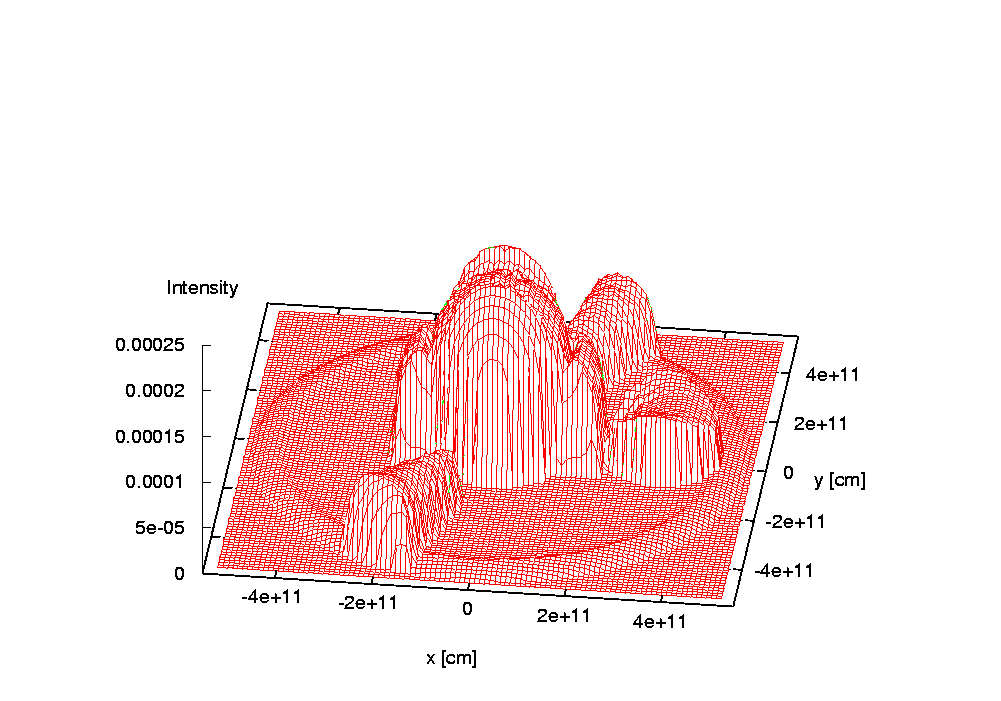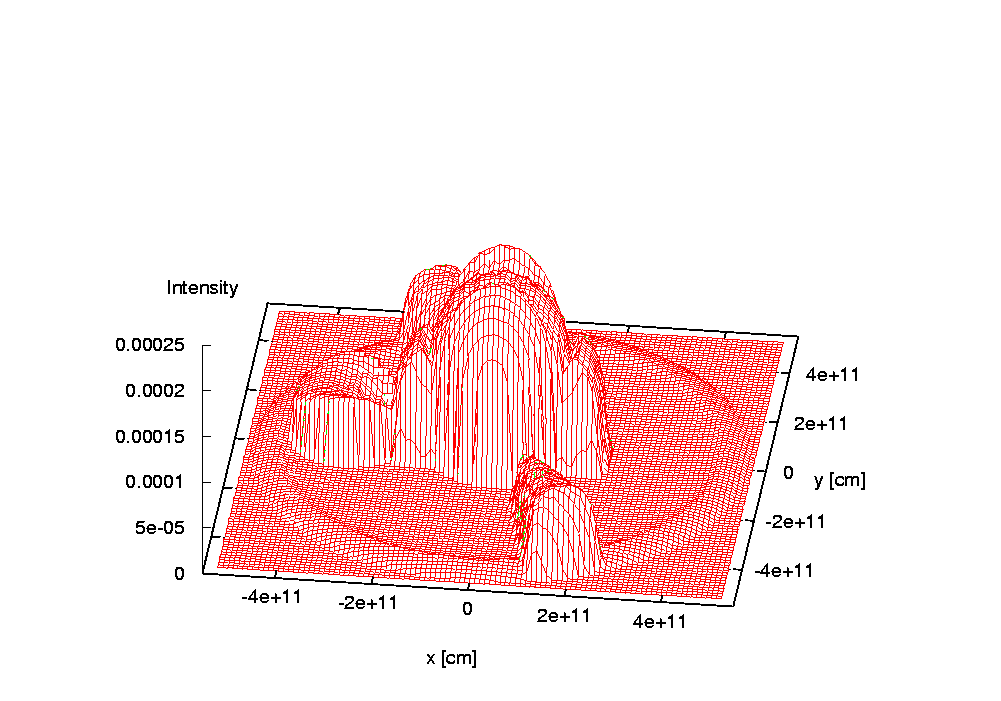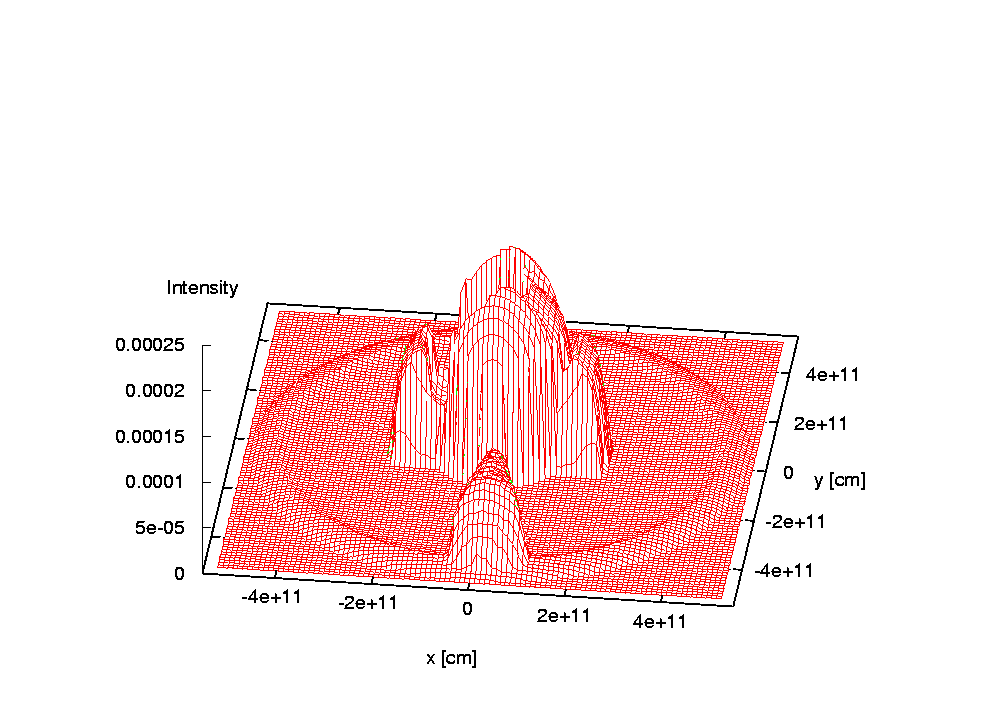
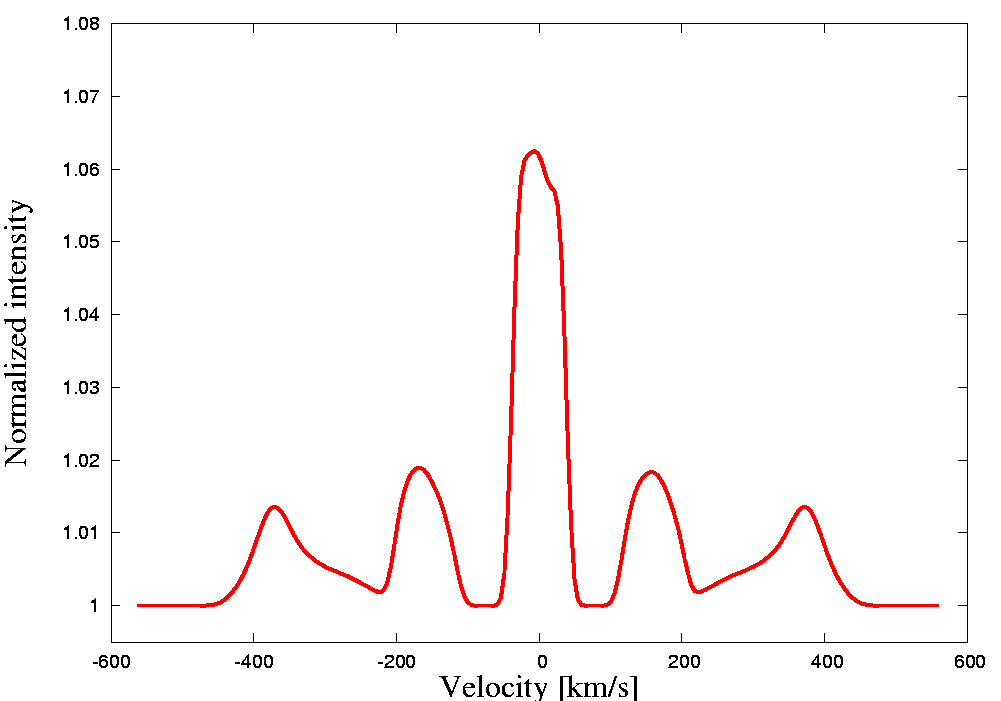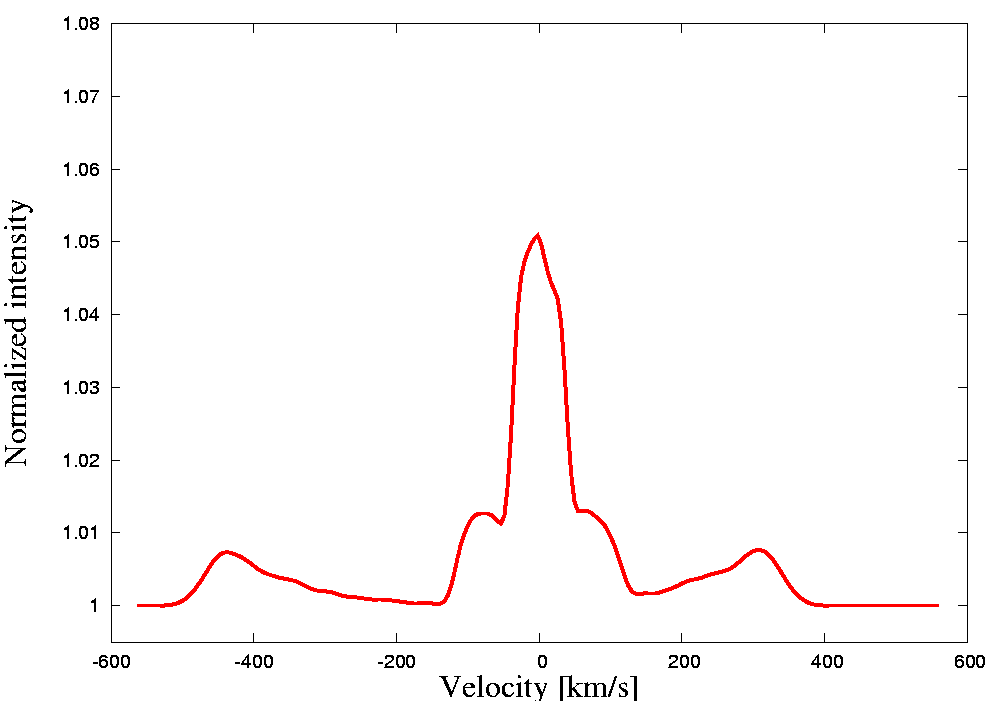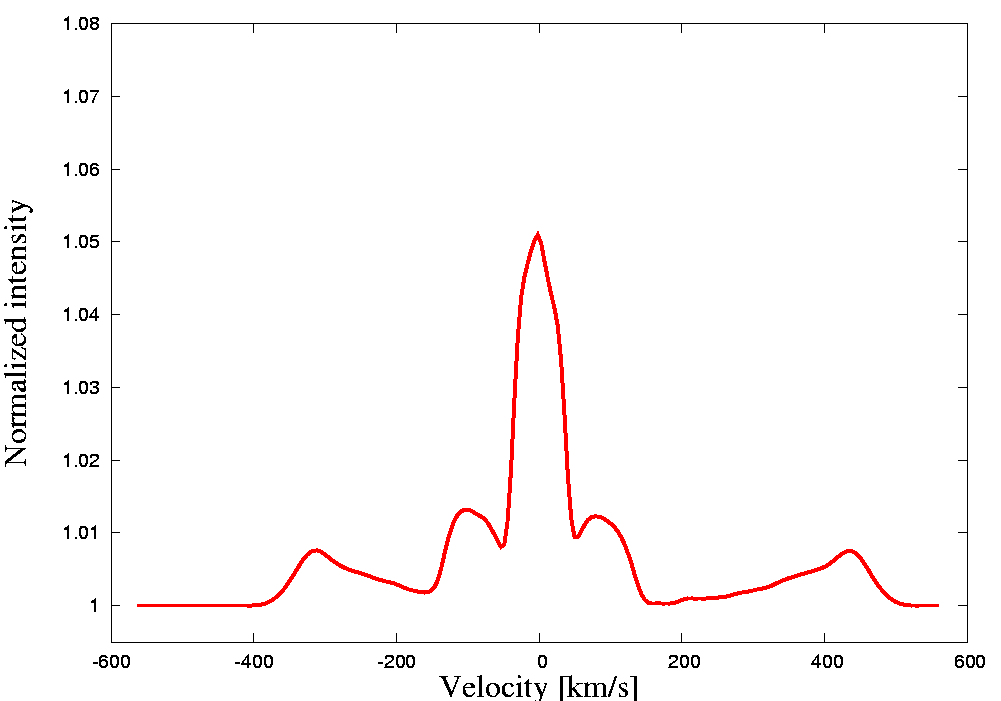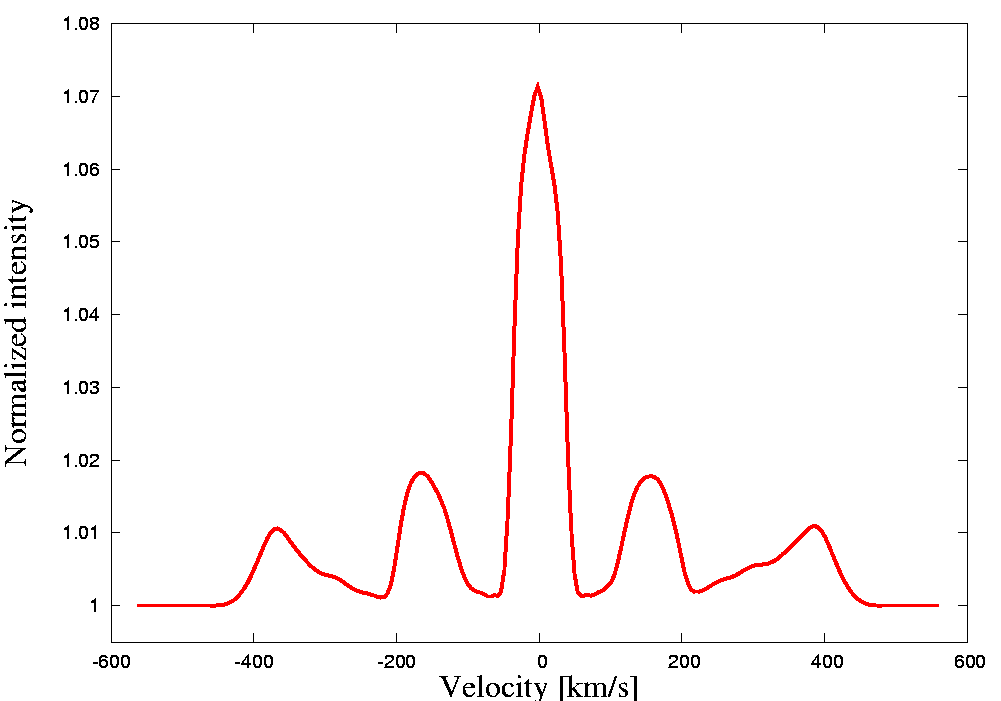
Last update: Oct 15, 2020